Amplitude modulation
| Passband modulation |
|---|
| Analog modulation |
| AM · SSB · QAM · FM · PM · SM |
| Digital modulation |
| FSK · MFSK · ASK · OOK · PSK · QAM MSK · CPM · PPM · TCM · SC-FDE |
| Spread spectrum |
| CSS · DSSS · FHSS · THSS |
| See also: Demodulation, modem, line coding, PAM, PWM, PCM |
Amplitude modulation (AM) is a technique used in electronic communication, most commonly for transmitting information via a radio carrier wave. AM works by varying the strength of the transmitted signal in relation to the information being sent. For example, changes in signal strength may be used to specify the sounds to be reproduced by a loudspeaker, or the light intensity of television pixels. Contrast this with frequency modulation, in which the frequency is varied, and phase modulation, in which the phase is varied.
In the mid-1870s, a form of amplitude modulation—initially called "undulatory currents"—was the first method to successfully produce quality audio over telephone lines. Beginning with Reginald Fessenden's audio demonstrations in 1906, it was also the original method used for audio radio transmissions, and remains in use today by many forms of communication—"AM" is often used to refer to the mediumwave broadcast band (see AM radio).
Contents[hide] |
Forms of amplitude modulation
In radio communication, a continuous wave radio-frequency signal (a sinusoidal carrier wave) has its amplitude modulated by an audio waveform before transmission. In the frequency domain, amplitude modulation produces a signal with power concentrated at the carrier frequency and two adjacent sidebands. Each sideband is equal in bandwidth to that of the modulating signal, and is a mirror image of the other. Amplitude modulation resulting in two sidebands and a carrier is called "double-sideband amplitude modulation" (DSB-AM). Amplitude modulation is inefficient in power usage; at least two-thirds of the power is concentrated in the carrier signal, which carries no useful information (beyond the fact that a signal is present).
To increase transmitter efficiency, the carrier may be suppressed. This produces a reduced-carrier transmission, or DSB "double-sideband suppressed-carrier" (DSB-SC) signal. A suppressed-carrier AM signal is three times more power-efficient than AM. If the carrier is only partially suppressed, a double-sideband reduced-carrier (DSBRC) signal results. For reception, a local oscillator will typically restore the suppressed carrier so the signal can be demodulated with a product detector.
Improved bandwidth efficiency is achieved at the expense of increased transmitter and receiver complexity by completely suppressing both the carrier and one of the sidebands. This is single-sideband modulation, widely used in amateur radio and other communications applications. A simple form of AM, often used for digital communications, is on-off keying: a type of amplitude-shift keying in which binary data is represented by the presence or absence of a carrier. This is used by radio amateurs to transmit Morse code and is known as continuous wave (CW) operation.
ITU designations
In 1982, the International Telecommunication Union (ITU) designated the types of amplitude modulation:
| Designation | Description |
|---|---|
| A3E | double-sideband a full-carrier - the basic Amplitude modulation scheme |
| R3E | single-sideband reduced-carrier |
| H3E | single-sideband full-carrier |
| J3E | single-sideband suppressed-carrier |
| B8E | independent-sideband emission |
| C3F | vestigial-sideband |
| Lincompex | linked compressor and expander |
Example: double-sideband AM
A carrier wave is modeled as a sine wave:
in which the frequency in Hz is given by:
The constants 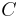 and
and 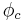 represent the carrier amplitude and initial phase, and are introduced for generality. For simplicity, their respective values can be set to 1 and 0.
represent the carrier amplitude and initial phase, and are introduced for generality. For simplicity, their respective values can be set to 1 and 0.
Let m(t) represent an arbitrary waveform that is the message to be transmitted, and let the constant M represent its largest magnitude:
The message might be just a simple audio tone of frequency:
It is assumed that 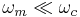 and that
and that ![\min[ m(t) ] = -M.\,](/2012-wikipedia_en_all_nopic_01_2012/I/54547769189712b4423fef366b166bd4.png)
Amplitude modulation is formed by the product:
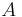 represents the carrier amplitude, which is a constant that demonstrates the modulation index. The values A=1 and M=0.5 produce y (t), depicted by the top graph (labelled "50% Modulation") in Figure 4.
represents the carrier amplitude, which is a constant that demonstrates the modulation index. The values A=1 and M=0.5 produce y (t), depicted by the top graph (labelled "50% Modulation") in Figure 4.
In this example, y(t) can be trigonometrically manipulated into the following (equivalent) form:
Therefore, the modulated signal has three components: a carrier wave and two sinusoidal waves (known as sidebands), whose frequencies are slightly above and below 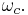
The choice A=0 eliminates the carrier component, but leaves the sidebands (DSBSC transmission). To generate a double-sideband full carrier (A3E) signal, we must choose:
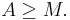
Spectrum
For more general forms of m(t), trigonometry is not sufficient; however, if the top trace of Figure 2 depicts the frequency of m(t) the bottom trace depicts the modulated carrier. It has two components: one at a positive frequency (centered on 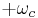 ) and one at a negative frequency (centered on
) and one at a negative frequency (centered on 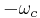 ). Each component contains the two sidebands and a narrow segment in between, representing energy at the carrier frequency. Since the negative frequency is a mathematical artifact, examining the positive frequency demonstrates that an AM signal's spectrum consists of its original (two-sided) spectrum, shifted to the carrier frequency. Figure 2 is a result of computing the Fourier transform of:
). Each component contains the two sidebands and a narrow segment in between, representing energy at the carrier frequency. Since the negative frequency is a mathematical artifact, examining the positive frequency demonstrates that an AM signal's spectrum consists of its original (two-sided) spectrum, shifted to the carrier frequency. Figure 2 is a result of computing the Fourier transform of: ![[A %2B m(t)]\cdot \sin(\omega_c t),\,](/2012-wikipedia_en_all_nopic_01_2012/I/13aaf1988439463e97c336085f44283d.png) using the following transform pairs:
using the following transform pairs:
Power and spectrum efficiency
In terms of positive frequencies, the transmission bandwidth of AM is twice the signal's original (baseband) bandwidth; both the positive and negative sidebands are shifted up to the carrier frequency. Thus, double-sideband AM (DSB-AM) is spectrally inefficient since fewer radio stations can be accommodated in a given broadcast band. The suppression methods described above may be understood in terms of Figure 2. With the carrier suppressed, there would be no energy at the center of a group; with a sideband suppressed, the "group" would have the same bandwidth as the positive frequencies of 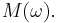 The transmitter-power efficiency of DSB-AM is relatively poor (about 33 percent). The benefit of this system is that receivers are cheaper to produce. Suppressed-carrier AM is 100 percent power-efficient, since no power is wasted on the carrier signal (which conveys no information).
The transmitter-power efficiency of DSB-AM is relatively poor (about 33 percent). The benefit of this system is that receivers are cheaper to produce. Suppressed-carrier AM is 100 percent power-efficient, since no power is wasted on the carrier signal (which conveys no information).
Modulation index
The AM modulation index is the measure of the amplitude variation surrounding an unmodulated carrier. As with other modulation indices, in AM this quantity (also called "modulation depth") indicates how much the modulation varies around its "original" level. For AM, it relates to variations in carrier amplitude and is defined as:
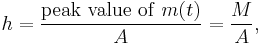 where
where 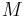 and
and 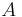 were introduced above.
were introduced above.
So if 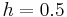 , carrier amplitude varies by 50% above (and below) its unmodulated level; for
, carrier amplitude varies by 50% above (and below) its unmodulated level; for 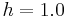 , it varies by 100%. To avoid distortion, modulation depth must not exceed 100 percent. Transmitter systems will usually incorporate a limiter circuit (such as a VOGAD) to ensure this. However, AM demodulators can be designed to detect the inversion (or 180-degree phase reversal) that occurs when modulation exceeds 100 percent; they automatically correct for this defect. Variations of a modulated signal with percentages of modulation are shown below. In each image, the maximum amplitude is higher than in the previous image (note that the scale changes from one image to the next).
, it varies by 100%. To avoid distortion, modulation depth must not exceed 100 percent. Transmitter systems will usually incorporate a limiter circuit (such as a VOGAD) to ensure this. However, AM demodulators can be designed to detect the inversion (or 180-degree phase reversal) that occurs when modulation exceeds 100 percent; they automatically correct for this defect. Variations of a modulated signal with percentages of modulation are shown below. In each image, the maximum amplitude is higher than in the previous image (note that the scale changes from one image to the next).
Modulation methods
Modulation circuit designs may be classified as low- or high-level (depending on whether they modulate in a low-power domain—followed by amplification for transmission—or in the high-power domain of the transmitted signal).[1]
Low-level generation
In modern radio systems, modulated signals are generated via digital signal processing (DSP). With DSP many types of AM modulation are possible with software control (including DSB with carrier, SSB suppressed-carrier and independent sideband, or ISB). Calculated digital samples are converted to voltages with a digital to analog converter, typically at a frequency less than the desired RF-output frequency. The analog signal must then be shifted in frequency, and linearly amplified to the desired frequency and power level (linear amplification must be used to prevent modulation distortion).[2] This low-level method for AM is used in many Amateur Radio transceivers.[3]
AM may also be generated at a low level, using analog methods described in the next section.
High-level generation
High-power AM transmitters (such as those used for AM broadcasting) are based on high-efficiency class-D and class-E power amplifier stages, modulated by varying the supply voltage.[4]
Older designs (for broadcast and amateur radio) also generate AM by controlling the transmitter’s final amplifier (generally a class-C, for efficiency) gain. The following types are for vacuum tube transmitters (but similar options are available with transistors):[5]
- Plate modulation: In plate modulation, the plate voltage of the RF amplifier is modulated with the audio signal. The audio power requirement is 50 percent of the RF-carrier power.
- Heising (constant-current) modulation: RF amplifier plate voltage is fed through a “choke” (high-value inductor). The AM modulation tube plate is fed through the same inductor, so the modulator tube diverts current from the RF amplifier. The choke acts as a constant current source in the audio range. This system has a low power efficiency.
- Control grid modulation: The operating bias and gain of the final RF amplifier can be controlled by varying the voltage of the control grid. This method requires little audio power, but care must be taken to reduce distortion.
- Clamp tube (screen grid) modulation: The screen-grid bias may be controlled through a “clamp tube”, which reduces voltage according to the modulation signal. It is difficult to approach 100-percent modulation while maintaining low distortion with this system.
Demodulation methods
The simplest form of AM demodulator consists of a diode which is configured to act as envelope detector. Another type of demodulator, the product detector, can provide better-quality demodulation with additional circuit complexity.
See also
- AM radio
- AM stereo
- Mediumwave band used for AM broadcast radio
- Longwave band used for AM broadcast radio
- Frequency modulation
- Shortwave radio almost universally uses AM, narrow FM occurring above 25 MHz.
- Modulation, for a list of other modulation techniques
- Amplitude modulation signalling system (AMSS), a digital system for adding low bitrate information to an AM signal.
- Sideband, for some explanation of what this is.
- Types of radio emissions, for the emission types designated by the ITU
- Airband
- Quadrature amplitude modulation
References
- ^ A.P.Godse and U.A.Bakshi (2009). Communication Engineering. Technical Publications. p. 36. ISBN 9788184310894. http://books.google.com/books?id=coQ6ac-fh6QC&pg=PA36.
- ^ Silver, Ward, ed (2011). "Ch. 15 DSP and Software Radio Design". The ARRL Handbook for Radio Communications (Eighty-eighth ed.). American Radio Relay League. ISBN 978-0-87259-096-0.
- ^ Silver, Ward, ed (2011). "Ch. 14 Transceivers". The ARRL Handbook for Radio Communications (Eighty-eighth ed.). American Radio Relay League. ISBN 978-0-87259-096-0.
- ^ Frederick H. Raab, et al (May 2003). "RF and Microwave Power Amplifier and Transmitter Technologies - Part 2". High Frequency Design: p. 22ff. http://www.scribd.com/doc/8616046/RF-Power-Amplifier-and-Transmitter-Technologies-Part2.
- ^ Laurence Gray and Richard Graham (1961). Radio Transmitters. McGraw-Hill. p. 141ff.
- Newkirk, David and Karlquist, Rick (2004). Mixers, modulators and demodulators. In D. G. Reed (ed.), The ARRL Handbook for Radio Communications (81st ed.), pp. 15.1–15.36. Newington: ARRL. ISBN 0-87259-196-4.
External links
- Amplitude Modulation by Jakub Serych, Wolfram Demonstrations Project.
- Amplitude Modulation, by S Sastry.
- Amplitude Modulation, an introduction by Federation of American Scientists.
- Amplitude Modulation tutorial video with example transmitter circuit.
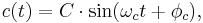
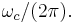
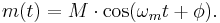
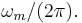
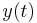
![= [1 %2B m(t)]\cdot c(t),\,](/2012-wikipedia_en_all_nopic_01_2012/I/d2744f51e7dfd22b6fe172de37db06ae.png)
![= A.[1 %2B M\cdot \cos(\omega_m t %2B \phi)]\cdot \sin(\omega_c t).](/2012-wikipedia_en_all_nopic_01_2012/I/a0c8fd8bde808ec44f375e1311818787.png)
![y(t) = A\cdot \sin(\omega_c t) %2B \begin{matrix}\frac{M}{2} \end{matrix} \left[\sin((\omega_c %2B \omega_m) t %2B \phi) %2B \sin((\omega_c - \omega_m) t - \phi)\right].\,](/2012-wikipedia_en_all_nopic_01_2012/I/a1941940efc3d9e97131c460c184b427.png)
![\begin{align}
m(t) \quad \stackrel{\mathcal{F}}{\Longleftrightarrow}&\quad M(\omega) \\
\sin(\omega_c t) \quad \stackrel{\mathcal{F}}{\Longleftrightarrow}&\quad i \pi \cdot [\delta(\omega %2B\omega_c)-\delta(\omega-\omega_c)] \\
A\cdot \sin(\omega_c t) \quad \stackrel{\mathcal{F}}{\Longleftrightarrow}&\quad i \pi A \cdot [\delta(\omega %2B\omega_c)-\delta(\omega-\omega_c)] \\
m(t)\cdot \sin(\omega_c t) \quad \stackrel{\mathcal{F}}{\Longleftrightarrow}& \frac{1}{2\pi}\cdot \{M(\omega)\} * \{i \pi \cdot [\delta(\omega %2B\omega_c)-\delta(\omega-\omega_c)]\} \\
=& \frac{i}{2}\cdot [M(\omega %2B\omega_c) - M(\omega -\omega_c)]
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/9df39d9e692859ed8660340e303bee8f.png)